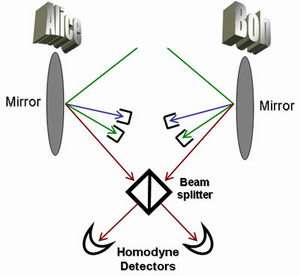
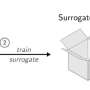
The scientists´ scheme for detecting macroscopic entanglement: two laser pulses reflect off two identical oscillators, exciting a vibrational mode which generates optical sideband modes. After a beam splitter mixes the "Stokes" modes (red), detectors perform measurements which turn the optomechanical entanglement into mechanical entanglement. Credit: Stefano Pirandola, et al.
Building upon recent studies on optomechanical entanglement with lasers and mirrors, a group of scientists has developed a theoretical model using entanglement swapping in order to entangle two micromechanical oscillators. This ability could lead to advances in information processing, as well as other applications that use micromechanical resonators, such as electrometers, displacement detectors, and radio frequency signal processors, wrote scientists Stefano Pirandola et al. in a recent Physical Review Letters.
"Until now, entanglement has been observed only for optical modes, i.e., photons (which are massless particles)," Pirandola told PhysOrg.com. "The significance of purely mechanical entanglement would be that it involves massive objects like mechanical oscillators (small vibrations on a mirror). Even though the oscillators must be small--their mass should be on the order of micrograms and their length around the micrometer--these sizes are 'macroscopic' for a quantum mechanical object."
The two entangled oscillators in Pirandola et al's proposed model are the mechanical components of two separate micro-opto-mechanical systems. Instead of entangling the oscillators directly, the scientists suggested entangling the optical parts of the systems--the reflected laser beams--and then used entanglement swapping to correlate the two oscillators.
In entanglement swapping, two objects that have correlated properties never meet directly; instead, a third party acts as a messenger between the two, swapping their properties as accurately as if they had directly interacted. One potential use for entanglement swapping is in quantum repeaters for future quantum computers, which would amp up the signal over long distances to prevent it from being buried by noise and dying out.
Earlier studies on optomechanical entanglement (extensively performed by the Univ. of Camerino group) demonstrated that radiation pressure from an intense laser beam shining on an oscillator could excite the oscillator's vibrational mode and yield two optical sideband modes induced by the vibrations. In the current scheme, when the two oscillators are positioned in such a way that their generated optical modes meet after reflecting, the beams could be mixed with a beam splitter.
Next, a "middleman" detection device would detect and mix the optical modes, and also perform measurements such as joined Homodyne detections, which are standard optical measurements for detecting radiation. When the detector performs these measurements, it can pass on the outcomes of the measurements to both the oscillators. Through this swapping, the entanglement changes from optomechanical to purely mechanical.
In addition to opening the doors to future applications, mechanical macroscopic entanglement would also demonstrate that mechanical systems made of atoms can exhibit quantum behaviour. Pirandola et al's calculations for quantum entanglement on a macroscopic scale, in a purely mechanical state, suggest that quantum phenomenon may not be as limited to the quantum world as scientists once thought.
"Would this theoretical scheme diminish the differences between the macroscopic and quantum worlds? This is a fundamental question of quantum mechanics," said Pirandola. "Whether or not there is a maximum size for oscillators that demonstrate entanglement is an open question right now. We don't know if there is some limit for the sizes of the objects to be entangled. Optimists think that it is only a matter of advances in quantum technologies."
Citation: Pirandola, Stefano, Vitali, David, Tombesi, Paolo, and Lloyd, Seth. "Macroscopic Entanglement by Entanglement Swapping." Physical Review Letters. 97, 150403 (2006).
By Lisa Zyga, Copyright 2006 PhysOrg.com