New theory broadens phase transition exploration

In a paper recently published in Physical Review Letters, Los Alamos National Laboratory researchers offer a new theory that predicts defect density across a variety of phase transitions. The research opens new routes for the exploration of defect formation in fields such as materials science, high-energy physics and cosmology.

"Phase transitions are a part of everyday life as well as fundamental phenomena in high-energy physics, inevitable in the early universe," said Fumika Suzuki, Los Alamos scientist and lead author on the paper. "Our study demonstrates that, when integrated with nucleation theory, the Kibble-Zurek mechanism proposed for second-order, or continuous, phase transitions can be extended to predict defect formation in a wider range of phase transitions."

First- and second-order phase transitions

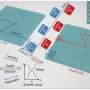
In first-order phase transitions, some parts of a system may enter the new phase before other parts—think of water boiling, with vapor bubbles forming as the water boils away. In second-order transitions, an entire system transitions at once. Systems such as superconductors and charged superfluids can experience second-order phase transitions that under the influence of external parameters (such as temperature or field) can develop first-order characteristics.

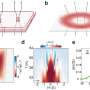
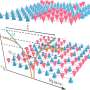
The Kibble-Zurek mechanism, co-named for Los Alamos physicist and paper co-author Wojciech Zurek, predicts the density of topological defects formed due to phase transitions, applying originally only to the second-order phase transitions.

But by integrating the Kibble-Zurek mechanism with nucleation theory, which describes the dynamics of symmetry breaking in first-order phase transitions, Suzuki and Zurek could extend the Kibble-Zurek mechanism to predict the density of defects formed in "tunable" phase transitions that combine characteristics of the phase transitions of first and second order.

The team's theory could be tested, for example, in the Fredericks phase transition in liquid crystals, which can be continuously tuned between first order and second order.